Math1013 Calculus I

Sine As a Function of Directed Angle in Radians

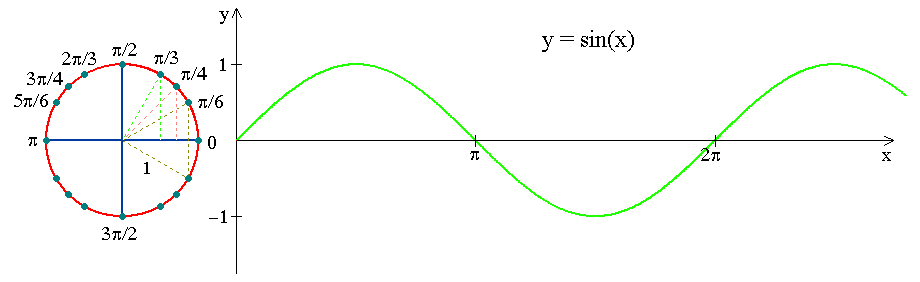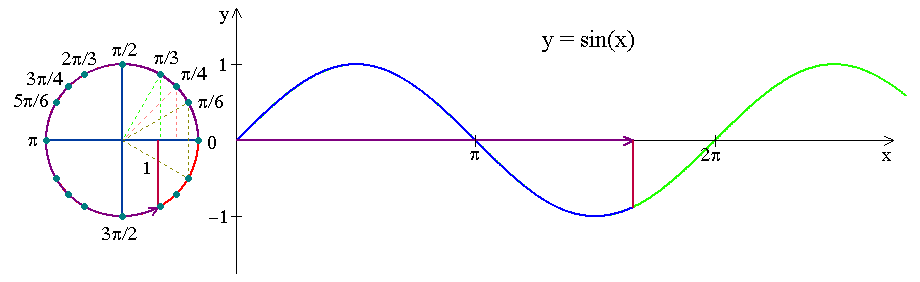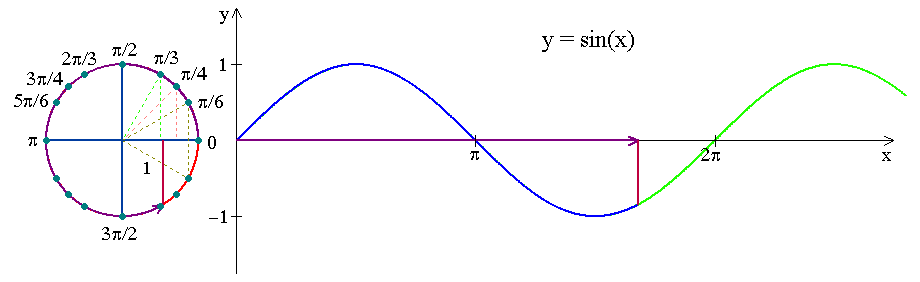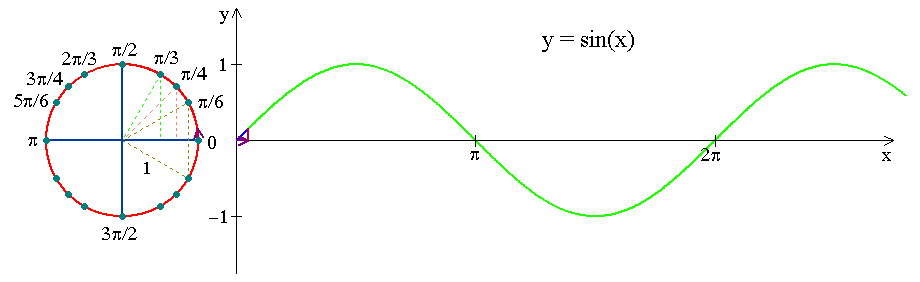
Look at how the  \(y\)-coordinate of a point running along a unit circle varies as a function of circular arc length travelled!

Notation: \(y=\sin x\)

Domain: \(-\infty <x<\infty\), i.e., the set of all real numbers (radian measures of directed angles)

Range: \(-1\le y\le 1\),  i.e., the interval \([-1,1]\)

Period = length of the unit circle = \(2\pi\)

An odd function:  \(\sin(-x) = - \sin x\)

\(x\) \(0\) \(\frac{\pi}{6}\) \(\frac{\pi}{4}\) \(\frac{\pi}{3}\) \(\frac{\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\pi\)
\(\sin x \) \(0\) \(\frac{1}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{\sqrt{3}}{2}\) \(1\) \(\frac{\sqrt{3}}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{1}{2}\) \(0\)
\(x\) \(-\pi\) \(-\frac{5\pi}{6}\) \(-\frac{3\pi}{4}\) \(-\frac{3\pi}{2}\) \(-\frac{\pi}{2}\) \(-\frac{\pi}{3}\) \(-\frac{\pi}{4}\) \(-\frac{\pi}{6}\) \(0\)
\(\sin x\) \(0\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{\sqrt{3}}{2}\) \(-1\) \(-\frac{\sqrt{3}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{1}{2}\) \(0\)

ˇ@

ˇ@

ˇ@

Recall \(180^\circ =\pi  \,\,  \mbox{(rad.)}  \).

Cosine As a Function of Directed Angle in Radians

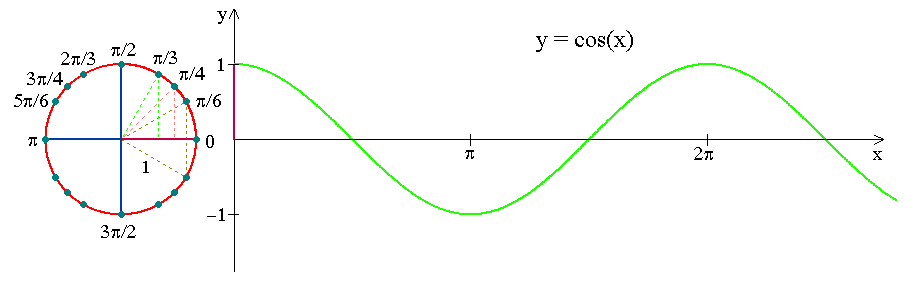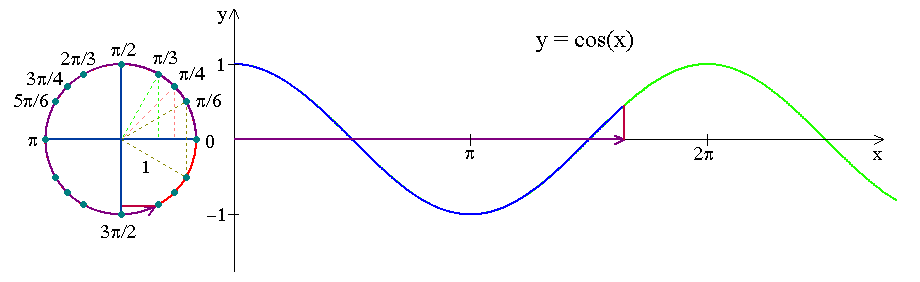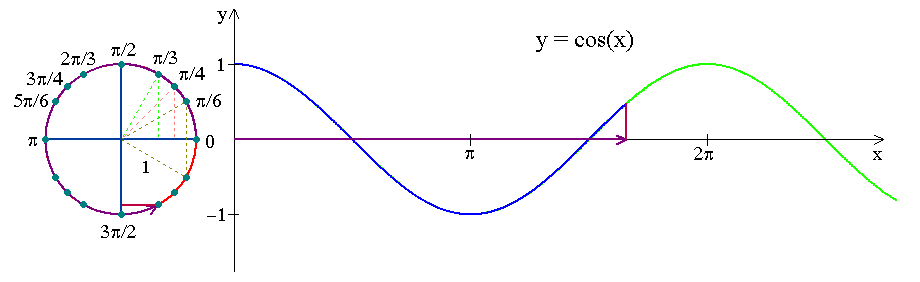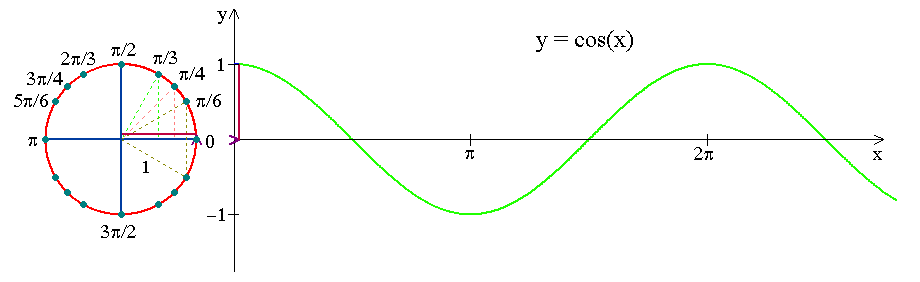
Look at how the \(x\)-coordinate of a point running along a unit circle varies as a function of circular arc length travelled!

Notation: \(y=\cos x\)

Domain: \(-\infty <x<\infty\), i.e., the set of all real numbers (radian measures of directed angles)

Range: \(-1\le y\le 1\),  i.e., the interval \([-1,1]\)

Period = length of the unit circle = \(2\pi\)

An even function:  \(\cos(-x) = \cos x\)

\(x\) \(0\) \(\frac{\pi}{6}\) \(\frac{\pi}{4}\) \(\frac{\pi}{3}\) \(\frac{\pi}{2}\) \(\frac{2\pi}{3}\) \(\frac{3\pi}{4}\) \(\frac{5\pi}{6}\) \(\pi\)
\(\cos x\) \(1\) \(\frac{\sqrt{3}}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{1}{2}\) \(0\) \(-\frac{1}{2}\) \(-\frac{\sqrt{2}}{2}\) \(\frac{\sqrt{3}}{2}\) \(-1\)
\(x\) \(-\pi\) \(-\frac{5\pi}{6}\) \(-\frac{3\pi}{4}\) \(-\frac{3\pi}{2}\) \(-\frac{\pi}{2}\) \(-\frac{\pi}{3}\) \(-\frac{\pi}{4}\) \(-\frac{\pi}{6}\) \(0\)
\(\cos x\) \(-1\) \(-\frac{\sqrt{3}}{2}\) \(-\frac{\sqrt{2}}{2}\) \(-\frac{1}{2}\) \(0\) \(\frac{1}{2}\) \(\frac{\sqrt{2}}{2}\) \(\frac{\sqrt{3}}{2}\) \(1\)

ˇ@

ˇ@

ˇ@

Exercise

Now, start running along a unit circle by starting at the point \( (0,0)\) and \((0,1)\) respectively, and answer the following questions.

(i) \(\sin(x+ \frac{\pi}{2}) = \cos x\) . Why?

(ii) \(\cos(\frac{\pi}{2} - x) = \sin x\) . Why?

Basic Trigonometric Identities

\(\begin{array}{lll} \cos^2 x +\sin^2 x =1, \qquad 1+\tan^2x=\sec^2x,\qquad 1+\cot^2x = \csc^2 x\\ \sin(A+B)=\sin A\cos B +\sin B\cos A\qquad\qquad \sin 2A = 2\sin A\cos B\\ \sin(A-B)=\sin A\cos B -\sin B\cos A\qquad\qquad \sin 3A = 3\sin A -4\sin^3 A \\ \cos(A+B)=\cos A\cos B -\sin A\sin B\qquad \qquad \cos 2A = \cos^2A -\sin^2A =2\cos^2A-1=1-2\sin^2A\\ \cos(A-B)=\cos A\cos B +\sin A\sin B\qquad\qquad \cos 3A = 4\cos^3 A -3\cos A\\ \sin A\cos B =\frac{1}{2}\big[\sin (A-B) +\sin (A+B)\big]\\ \sin A\sin B = \frac{1}{2}\big[\cos(A-B)-\cos (A+B)\big]\\ \cos A\cos B =\frac{1}{2}\big[\cos (A-B)+\cos (A+B)\big] \end{array}\)

Exercise

Note that \(\cos(A+B)=\cos A\cos B -\sin A\sin B\) if and only if \[\big(\cos(A+B)-1)^2+\sin^2(A+B) = \big(\cos A -\cos (-B)\big)^2+\big(\sin A -\sin (-B)\big)^2 \] where the left hand side is the distance between the points \((\cos(A+B),\sin (A+B))\) and \( (1,0)\), and the right hand side is the distance between the points \((\cos A,\sin A)\) and \((\cos (-B), \sin (-B))\).

(i) Now draw the points \((\cos A,\sin A)\), \((\cos (-B), \sin (-B))\) and \((\cos(A+B),\sin (A+B))\) on the unit circle centered at the orgin and see what this identity means.

(ii) Use this angle sum formula for consine to derive the other angle sum and angle difference formulas.

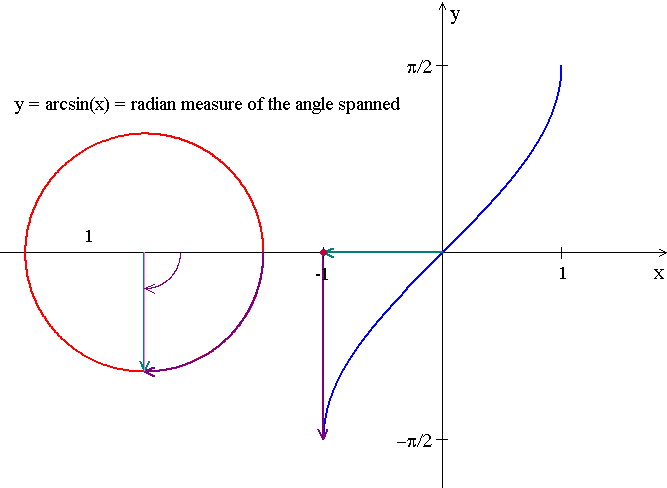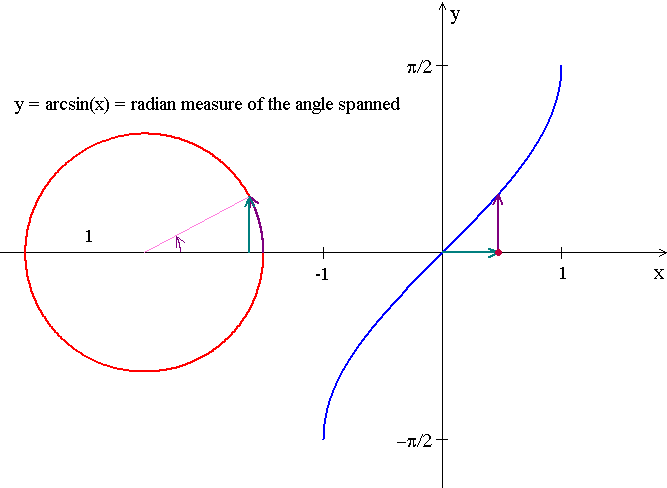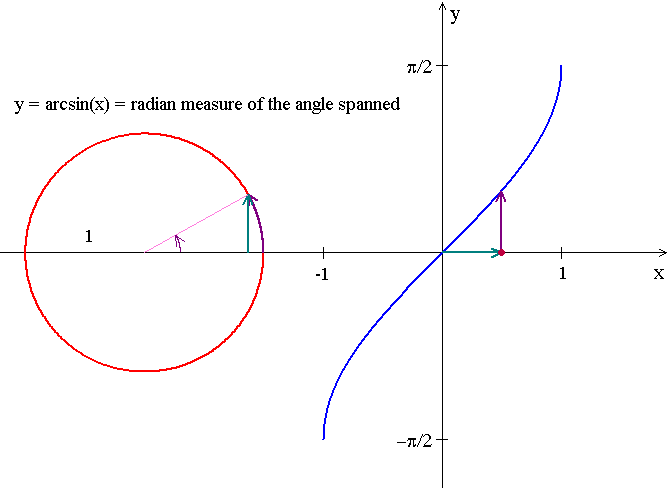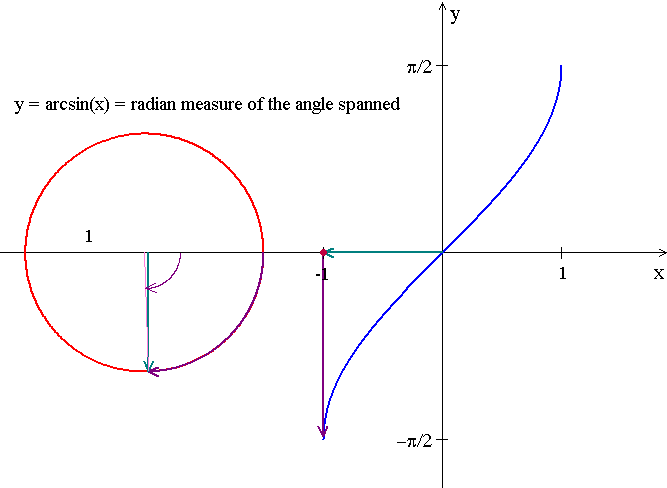
Graphing y= sin-1 x = arcsin(x) and y = cos-1 x = arccos(x)

Domain: [-1, 1]

Range: [-Łk/2, Łk/2]

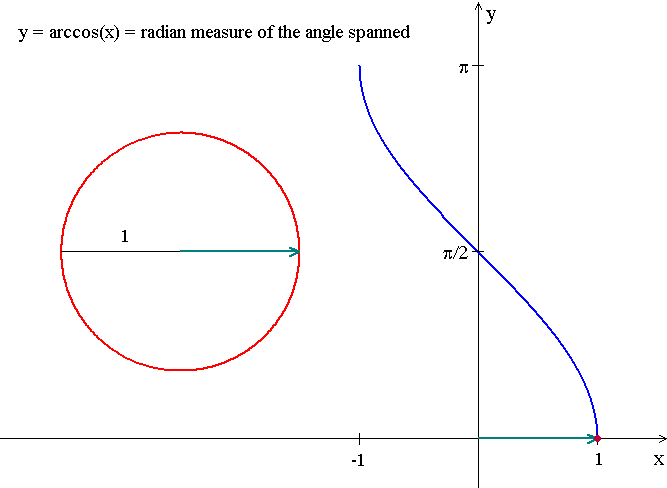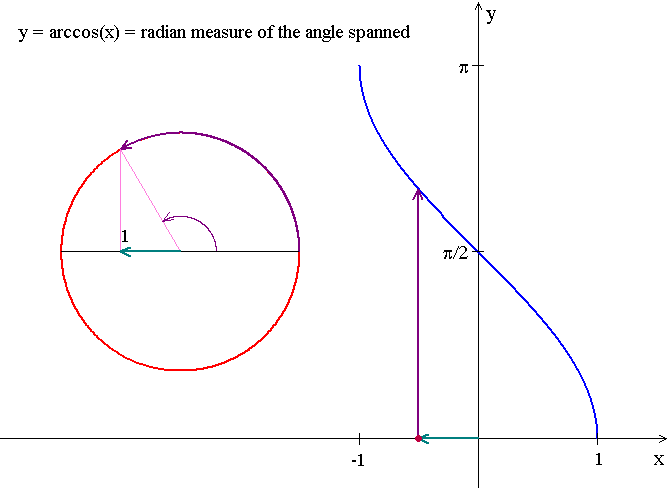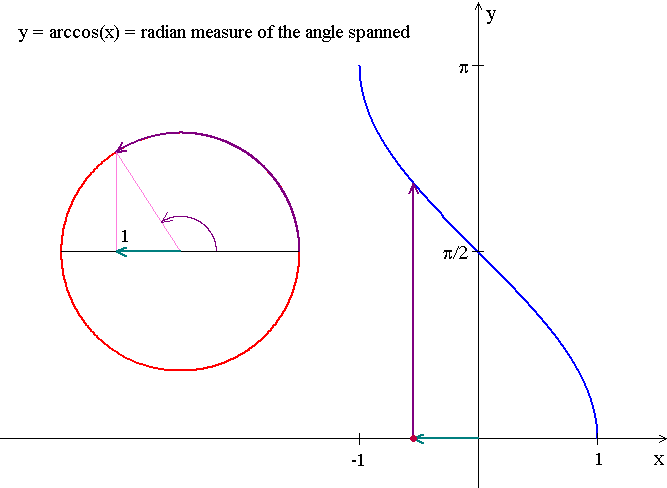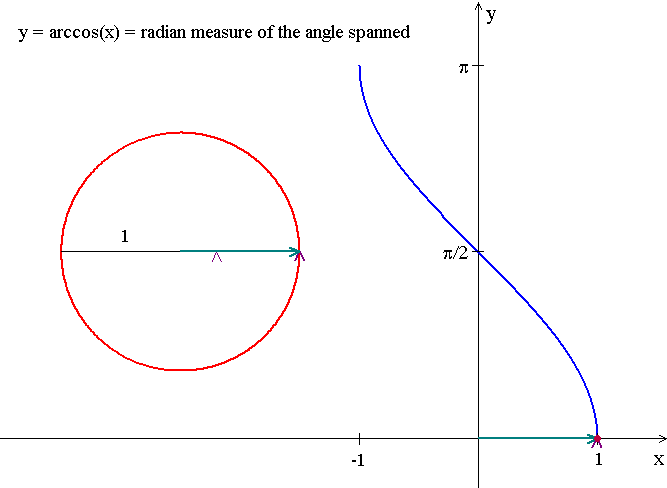
Domain: [-1, 1]

Range: [0, Łk]

Derivatives of Sine, Cosine and Other Trigonometric or Inverse Trigonometric Functions

\( \begin{array}{lllll} \dfrac{d\sin x}{dx} = \cos x&\qquad\qquad&\dfrac{d\csc x}{dx} = -\csc x\cot x&&\dfrac{d\sin^{-1}x}{dx}=\dfrac{1}{\sqrt{1-x^2}} \\ \dfrac{d\cos x}{dx} = -\sin x&&\dfrac{d\sec x}{dx}=\sec x\tan x&&\dfrac{d\cos^{-1}x}{dx}=-\dfrac{1}{\sqrt{1-x^2}}\\ \dfrac{d\tan x}{dx} = \sec^2 x &&\dfrac{d\cot x}{dx} = -\csc^2 x&\qquad&\dfrac{d\tan^{-1}x}{dx}=\dfrac{1}{1+x^2} \end{array} \)

Using suitable differentiation rules, e.g., quotient rule, chain rule or implicit differentiation, all these derivative formulas can be derived from the first one, i.e., \(\dfrac{d\sin x}{dx} = \cos x\).