My Research Interest:

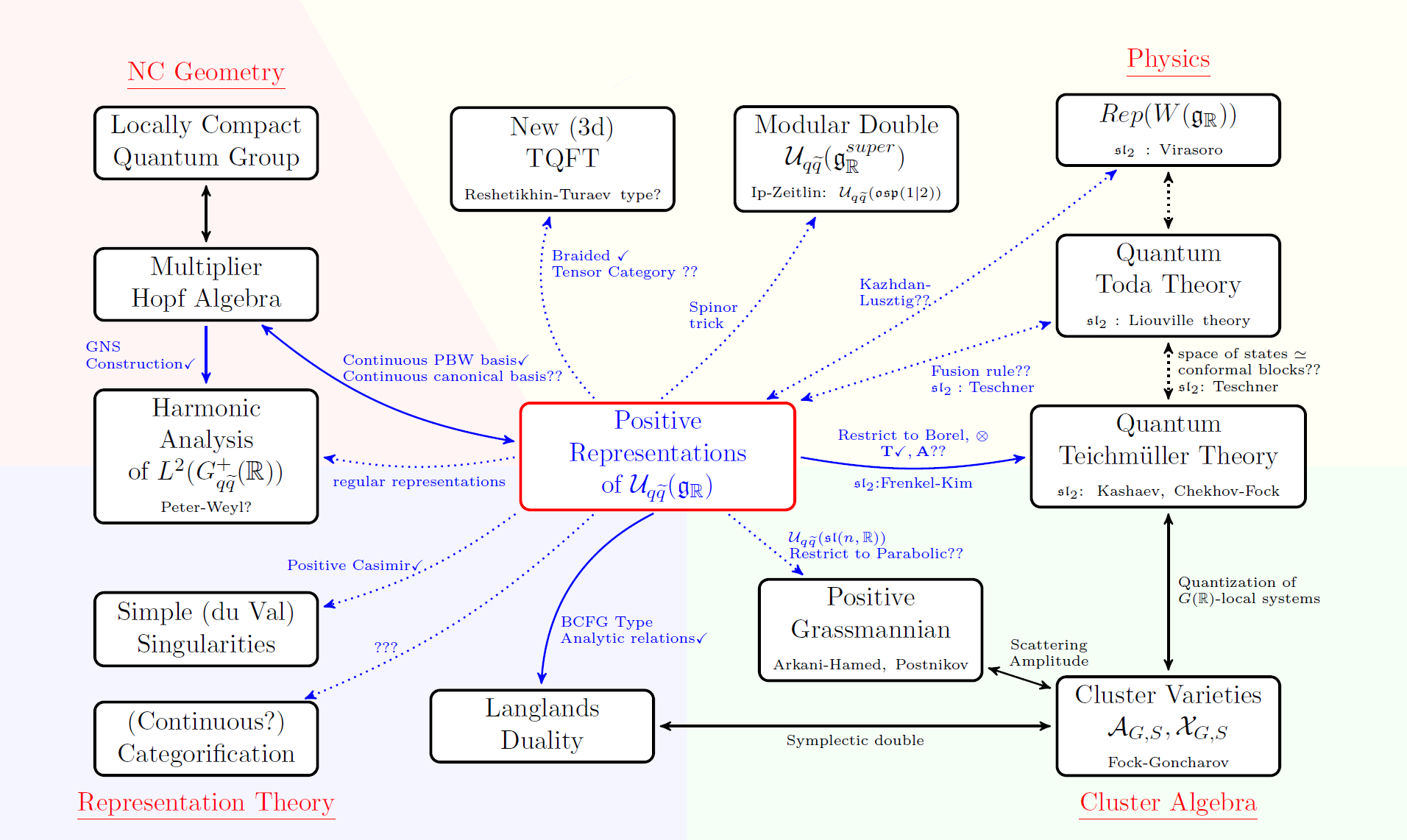
My research lies in the intersection of representation theory, non-commutative geometry, functional analysis and mathematical physics. Specifically, my research focuses on the theory of positive representations, which is a new research program devoted to the study of representation theory of split real quantum groups motivated from certain integrable systems.

The whole program involves several related theories, including Faddeev's modular double, the quantum dilogarithm and q-special functions, harmonic analysis on semigroup, cluster algebras, Lusztig's parametrization of total positivity, C*-algebra and unbounded operators. It is expected to have applications to construction of new TQFT's, categorifications, and quantum Teichmüller theory.

The current status of the research program and its future perspectives and applications to other areas of mathematics and physics is partially summarized in the following picture (click to enlarge).

My Research Statement (October 2016)